Function approximation and representation learning in RL
Is Q learning guaranteed to find optimal policy?
The answer is, yes, Q-learning finds an optimal policy for any finite Markov decision process. (Finite state, action and rewards sets, not finite episode.)
But for deep Q learning, the answer is no, partly due to function approximation, known as one of the “deadly triad”.
The heart of RL lies in learning value function, recursively defined by Bellman equation.
The Bellman equation is linear equation that can be solved directly (closed form).
Consider matrix form :
\[\begin{aligned} V &= R + \gamma P V \\\\ (I - \gamma P) V &= R \\\\ V &= (I - \gamma P)^{-1} R \end{aligned}\]However, this requires dynamics model $P$, and full sweep of $s \in S$.
For control problems, we consider Q function,
\[V_*(s)=max_a Q_*(s,a)\]Q function can be described by a table, for example :
\[\begin{array}{c|ccc} \text{State} \backslash \text{Action} & a_0 & a_1 \\ \hline s_0 & Q(s_0, a_0) & Q(s_0, a_1) \\ s_1 & Q(s_1, a_0) & Q(s_1, a_1) \\ \end{array}\]In real-world cases, the rows of Q table grows enormously.
Consider the game of Go (바둑), where the board has 19 x 19 positions and three stone types: empty, black, white. It yields $|S|=3^{19 \times 19} \approx 2 \times 10^{170}$ states. (Atoms of universe is considered $10^{80}$)
Therefore, we seek to find an approximation to Q function, such as in DQN : $Q(s,a) \approx \hat{Q}_\theta(\phi (s),a)$.
(Please refer to my other post for TD and Bellman equation.)
Deep model $f_{\phi}$ is widely used as encoder (feature extractor),
but how do we determine the ideal representational capacity?, i.e., how large should the network be?
Representation Learning – directly taken from value-improvement path. I really really like the Figure 1.
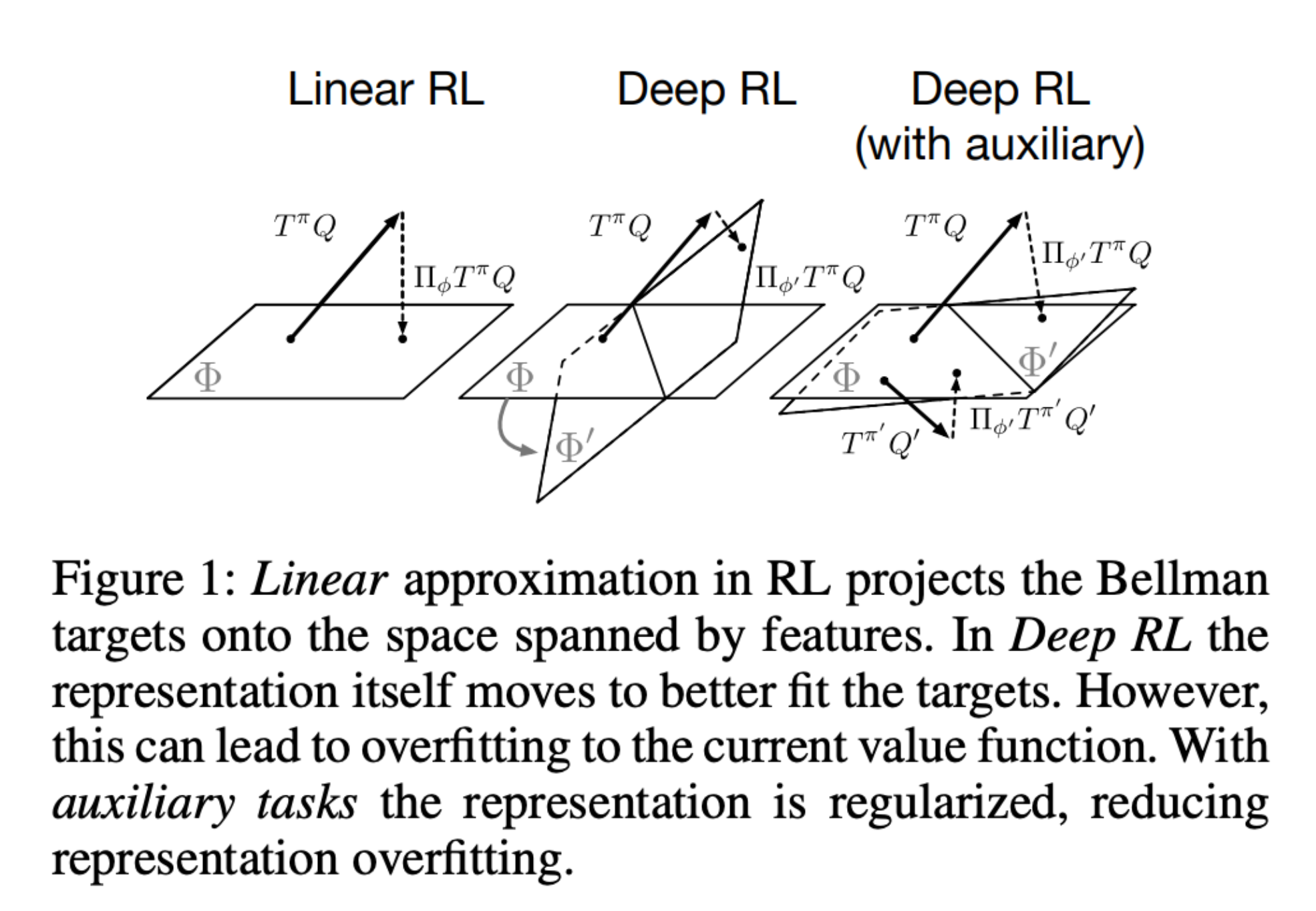
Usually, the state-action space $S \times A$ is too big to allow for an explicit representation of the functions $Q^\pi$, so one must resort to an approximation $\hat{Q}^\pi$.
A common approach is to parametrize:
\[\hat{Q}^\pi(s, a) = \phi(s)^\top \theta_a,\]where $\phi : S \rightarrow \mathbb{R}^K$ are features, $\theta_a \in \mathbb{R}^K$ are modifiable parameters associated with each $a \in A$, and $K \in \mathbb{N}$.
Given a set of (possibly non-linear) features $\phi : S \rightarrow \mathbb{R}^K$, policy evaluation comes down to computing the linear weights $(\theta_a \mid a \in A)$ such that $\hat{Q}^\pi \approx Q^\pi$.
This involves the projection of the Bellman operator onto the space spanned by $\phi$, denoted:
The problem of constructing the basis functions $\phi$ is known as representation learning.
Generally, $K \ll |S|$, so for a fixed $\phi$, the space of expressible value functions is much smaller than the space of all possible value functions.
Intuitively, then, a well-trained map $\phi$ should be such that $\phi(s)$ captures the salient information of $s \in S$ for return.
As long as the network has sufficient representational capacity, given enough training experience the learned representation $\phi(s)$ will be able to approximate a policy’s value function arbitrarily well.
I’ve been focusing on the weight dynamics of deep RL.
Consider rank, the number of independent bases, and magnitude $|| \cdot ||$ of representation $\Phi$.
As seen in Figure 1., the representation itself moves in deep RL.
The encoder of an agent should remain “plastic” during training process, s.t. it is able to learn unseen observations by keeping important features $\phi_i$ and discarding unimportant features $\phi_j$.
But the encoder might be overfitted to early experiences collected and be unable to learn from new experiences. The phenomena is called “loss of plasticity”.
This problem is important considering the recent trend of utilizing pre-trained model (so-called foundation model) as encoder for decision layers.
I hypothesized that given overparameterized encoder $f_{\phi}$, the rank should adaptively change so that the representation learnt is low-rank solution.
But what if we preserve the rank to fully utilize the capacity. For example we might promote the weight to preserve orthogonality by adding regularization term $||{\Phi}^T {\Phi} - I||$. However, this is computationally expensive, so I’m searching for other method to fully utilize the capacity given.
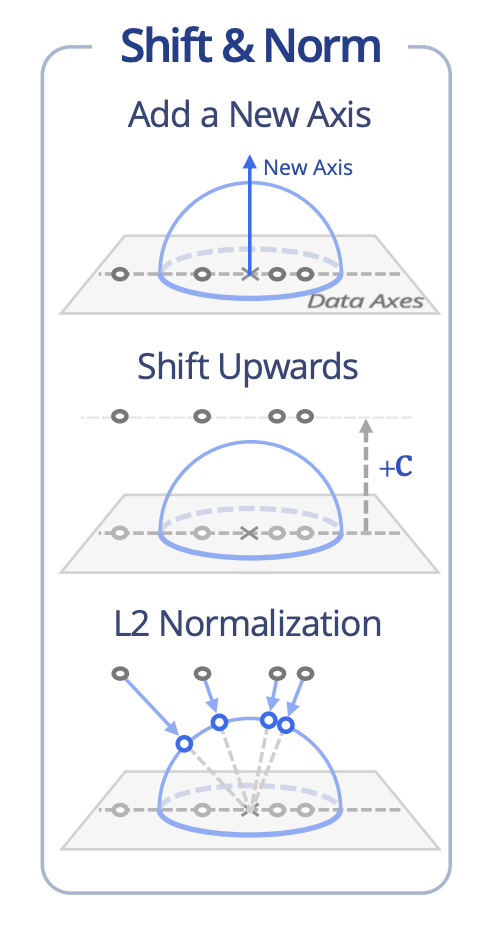
The magnitude of weight is already well-studied through literatures like weight regularization or normalization. For normalization, I had this question “can’t we track the weight magnitude somehow?”.
Below does not track the magnitude but instead, add an axis to express the magnitude on unit ball. What a brilliant idea!
Reference