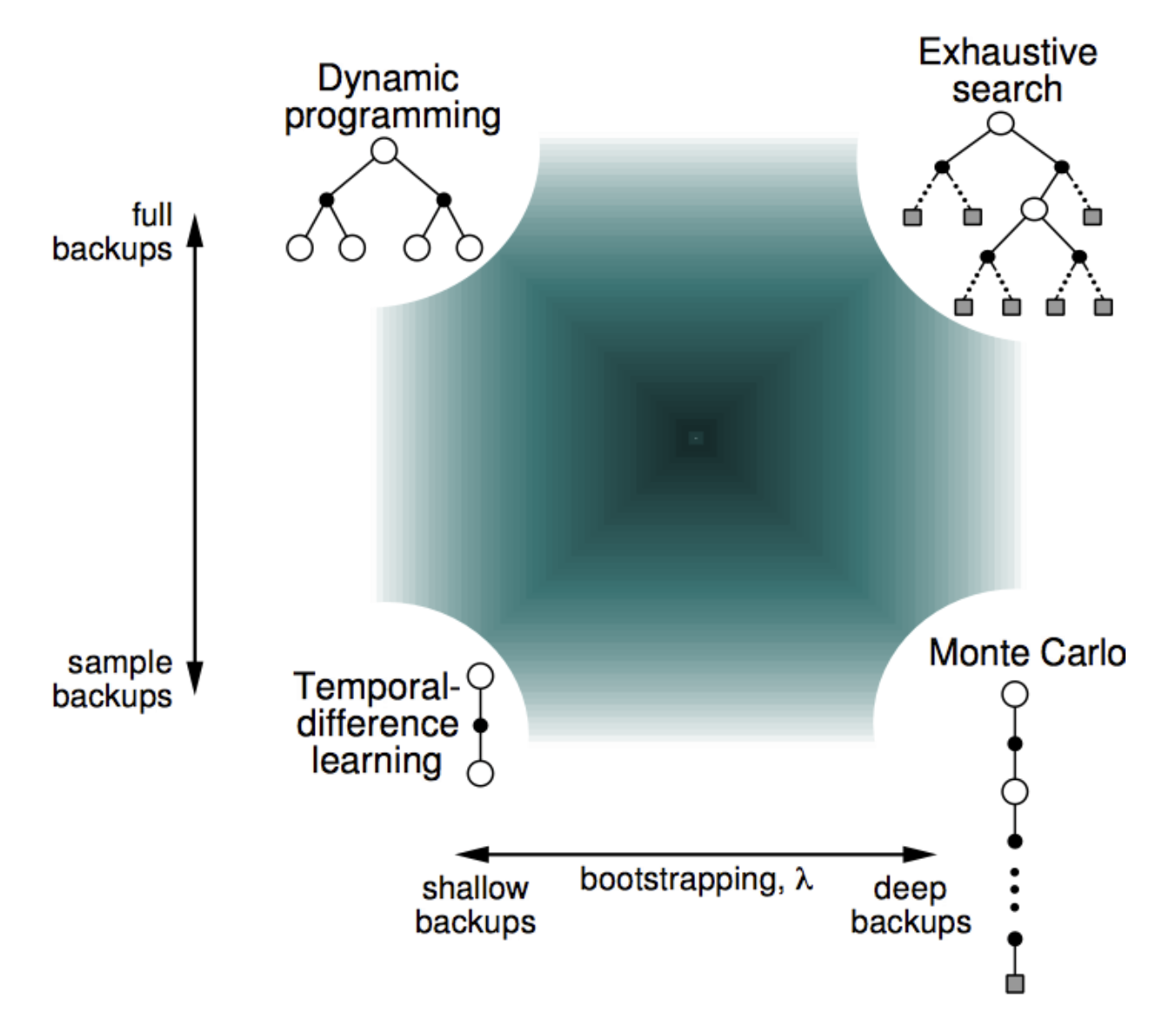
Updates :

Monte Carlo : $S_t \mapsto G_t$,

TD(0) : $S_t \mapsto R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}_t)$

$n$-step TD : $S_t \mapsto G_{t:t+n}$

DP : $s \mapsto \mathbb{E}_\pi \left[ R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}_t) \mid S_t = s \right]$

An operator is generally a mapping of function to function.

\[TV = R + \gamma PV\]

Bellman operator $T$ maps (updates) $V_t$ to $V_{t+1}$ by solving the recursive relationship.

As a relief, under complete metric space, applying $T$ repeatedly converges to unique solution at linear rate of $\gamma$, i.e. contraction mapping theorem, $||T(u)-T(v)||_{\infty} \leq \gamma ||u-v||_{\infty}$.

(Model-free, temporal difference, sample-based)

Temporal difference (TD) – literally, “temporal” difference between $t+1$ and $t$.

\[Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ \textcolor{red}{r_{t+1} + \gamma \max_a Q(s_{t+1}, a)} - Q(s_t, a_t) \right]\]

Analogously to “target” or label in supervised learning, TD “target” serves as a (semi-)supervision in Q learning.

TD target $r_{t+1} + \gamma \max_a Q(s_{t+1}, a)$ consists of : actual signal (label) $r_{t+1}$, estimation $\gamma \max_a Q(s_{t+1}, a)$.

Intuitively, Q function is updated by the error = (label + estimation) - (estimation); This is called “bootstrapping”; you estimate based on your estimation. c.f. Monte-Carlo method.

I was once obsessed with reducing the volume of $|S \times A|$, specifically $|A|$, but was it correct approach?